Общие положения

Современные посевные машины как и многие другие мобильные сельскохозяйственные агрегаты, представляют собой сложные управляемые динамические системы, функционирование которых протекает в условиях непрерывно изменяющихся внешних воздействий, обусловленных многочисленными и разнообразными факторами. В своем большинстве эти факторы являются случайными (в вероятностно-статистическом смысле), что, естественно, накладывает отпечаток случайности и на конечные показатели технологических процессов, выполняемых посевными машинами.

В связи с этим при решении задач, связанных с выбором и обоснованием параметров посевных машин, а также режимов их работы, применение методов классической механики, основанных на строго детерминированных закономерностях протекания рабочих процессов, является недостаточным, а нередко и невозможным, так как условия работы этих машин значительно сложнее и разнообразнее.

В последнее время для описания поведения, анализа и синтеза сельскохозяйственных машин начинают широко использоваться вероятностно-статистические методы, и в первую очередь методы теории случайных процессов. Этому в значительной мере способствовали основополагающие труды по динамике сельскохозяйственных агрегатов П. М. Василенко, А. Б. Лурье, А. П. Иофинова, А. П. Терехова, В. П. Рослякова, В. А. Ксендзова, С. В. Кардашевского и других авторов [70, 103, 205, 264, 284, 285].

В основе вероятностно-статистических методов исследования лежит построение математических  моделей, имитирующих с той или иной степенью точности поведение (функционирование) реальных объектов.

Применительно к решению задач анализа или синтеза сложных технических систем, в частности сельскохозяйственных машин, в основу построения моделей положена предпосылка о том, что в условиях нормального функционирования они (технический объект) представляют собой динамическую систему, осуществляющую некоторое преобразование входных переменных (возмущений) в выходные, которые показывают, как работает машина в условиях нормальной эксплуатации.

В общем случае расчетная схема сельскохозяйственных агрегатов представляется в виде многомерной динамической системы, на входе которой действуют (рис. 4.1) векторы-функций условий работы (возмущений) X = {x1 (t), x2 (t), ..., xn (t)} и управления U = {u1 (t), u2 (t), ..., uk (t)}. Вектор U является выходным для управляющих устройств, образующих в общем случае управляющую систему. С управляющей системой связано и задающее воздействие, т.е. вектор-функция Z = {z1 (t), z2 (t), ..., ze (t)}, показывающая, как должен себя вести управляемый объект. Выходные переменные обычно даются также в виде вектор-функции Y = {y1 (t), y2 (t), ..., ym (t)}, характеризующей поведение машины в действительных реальных условиях эксплуатации, то есть эта вектор-функция определяет технологические, энергетические и другие показатели работы машины или системы управления в целом.

Рис. 4.1. Структурная схема функционирования сельскохозяйственной машины.

Число составляющих n, k, l, m векторов зависит от типа машины, системы учета ее работы и других факторов,обусловленных целью и характером поставленной задачи. Они определяют фактический объем и содержание информации, на основе которых будет разрабатываться и реализовываться математическая модель.

Входные и выходные переменные для абсолютного большинства сх агрегатов, в том числе и для посевных машин, являются случайными процессами и при анализе их работы каждому входному процессу ставят в соответствие другой - выходной процесс. Если на входе машины действует переменная x (t), а на выходе y (t), то математическое описание поведения машины как одномерной системы представляется зависисмостью y (t) = A[x (t)], где А - оператор системы, показывающий, какие математические действия необходимо выполнить, чтобы по заданной функции x (t) определить выходной процесс y (t).

Построение математической модели машины и заключается в установлении (выборе) вида оператора А, связывающего входные x (t) и выходные y (t) переменные.

Нахождение оператора (построение математической модели) производится различными методами - теоретическими и экпериментальными. Сущность первого состоит в том, что сложную систему приводят к более простой (эквивалентной), позволяющей описать ее поведение аналитическими методами, например, при помощи дифференциальных уравнений динамики системы материальных точек.

Для большинства сх машин теоретическое построение математической модели представляет собой весьма трудную, а подчас и неразрешимую задачу. В этих случаях обычно прибегают к экпериментальным методам и, в основном, к методам идентификации, которые базируются на опытной информации о входных и выходных процессах машин, полученной в условиях нормального функционирования.

При использовании метода идентификации сх машины рассматриваются как линейные стационарные системы, а операторы, устанавливающие связь между выходным процессом y (t) и входным x (t), представляются в различных формах: алгебраических, дифееренциальных, интегральных или других видов функциональных уравнений.

При исследовании сх агрегатов в качестве операторов обычно принимаются:
а) передаточная функция W(s), так что y (s) = W (s) * x (s), (4.2.), где x (s) и  y (s) - изображения по Лапласу входной и выходной переменных;
б) частотная передаточная функция W (iω), которая определят свойства машины в частотной области;
в) импульсная переходная функция ω (t), определяющая свойства машины во временной области, причем 

(4.3);
г) линейное дифференциальное уравнения с постоянными коэффициентами вида
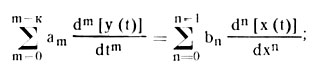(4.4);
д) линейный оператор интегрирования 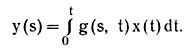(4.5).

Эти операторы характеризуют в конечном счете одни и те же свойства машины как динамической системы. При случайных входных и выходных переменных операторами могут служить и уравнения, связывающие математические ожидания выходных переменных относительно входных (уравнения регрессии).

Если входная x (t) и выходная y (t) функции являются стационарными случайными процессами, то связь между статистическими характеристиками этих процессов осуществляется через оператор 

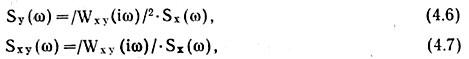
где Sx (ω) и Sy (ω) -спектральные плотности процессов; Sxy  - взаимная спектральная плотность входного и выходного процессов; |Wxy (iω)| = Axy (ω) - амплитудная частотная характеристика машины по отношению к входу x(t).

Из соотношения (4.6) получается 

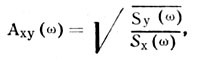  (4.8.)

а из соотношения (4.7)

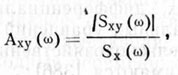(4.9)

причем   - модуль взаимной спектральной плотности входа x (t) И выхода y(t).

Соотношения (4.8) и (4.9) широко используются для определения частотных характеристик и передаточных функций сх машин по результатам их испытаний в условиях нормального функционирования. Так, в частности, для ряда машин по соотношениям (4.8) и (4.9) на основе значительного статистического материала было установлено, что передаточные функции этих машин и их рабочих органов относительно характерных входных воздействий, наблюдаемых в реальных условиях эксплуатации, могу быть представлены в первом приближении как

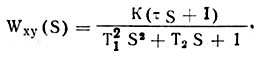  (4.10)

или
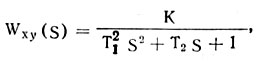(4.11)

где τ, Т1 и Т2 - постоянные времени; К - коэффициент усиления.

Таким образом, построение одномерной математической модели машины рассматриваемым методом сводится к выполнению следующих операций: а) экспериментальной  (в условиях нормальной эксплуатации) записи процессов x (t) и y (t) на входе и выходе машины; б) вычислению спектральных плотностей процессов; в) определению по соотношениям (4.8) и (4.9) амплитудной частотной характеристики Axy (ω); г)  аппроксимации характеристики Аху(со) аналитическим выражением, которому соответствует чаще всего передаточная функция вида (4.10) и (4.11); д) вычислению коэффициентов передаточных функций.

Для выполнения указанных операций обычно составляются ал­горитмы и программы вычислений на ЭЦВМ с использованием ансамблей реализации входных и выходных случайных процессов x(t)Hy(t).

Несмотря на большое значение и ценность математических моделей, составленных по методу идентификации для решения за­дач анализа и синтеза сельскохозяйственных машин, они являются весьма приближенными и не дают достаточных оснований для прогнозирования выходных процессов (показателей работы) и управления ими в условиях нормального функционирования, так как в действительности машины представляют собой сложные многомерные динамические системы, которым свойственны нали­чие внутренних помех (отказов), непостоянство параметров дина­мических характеристик, нелинейность связей, нестационарность возмущающих воздействий и т. д. Кроме того, по этим моделям в ряде случаев не представляется возможным прогнозировать по­ведение системы вне области изменения переменных, для которых были получены экспериментальные данные.

Поэтому при определении операторов возникает необходи­мость оценить, в какой мере выходная переменная y(t) согласо­вана с выбранным для модели входным воздействием x(t), т. е. оценить степень достоверности модели, построенной с учетом принятых априори допущений относительно ее структуры и ха­рактера возмущающих воздействий.

Основным и наиболее существенным недостатком вышеуказан­ных математических моделей является то, что они, в целом ха­рактеризуя динамические свойства рассматриваемой системы в различных условиях, не отражают связей выходных переменных (показателей работы) с ее конкретным конструктивным строе­нием, т. е. с геометрическими и режимными параметрами эле­ментов, составляющих данную систему. Иначе говоря, экспери­ментально полученные операторы не «расшифрованы» (не увя­заны) через параметры изучаемых систем (машины, агрегата, узла и т. д.), что лишает возможности использования их при проектировании и расчете новых машин и их рабочих органов.

Против этого можно возразить указанием на то, что при раз­работке модели (оператора) системы в состав составляющих векторов-функций F, и и Z условий работы (входных возмущений), управления и задающего воздействия (см. рис. 4.1) следует вклю­чать все или большинство предполагаемых априори факторов,которые в той или иной мере оказывают влияние на составляющие —>вектора-функции Y, и рассматривать машину (агрегат и т. д.) как многомерную динамическую систему, что позволит определить ее поведение в целом и даст возможность установить совокупное и раздельное влияние выбранных (заданных) входных факторов на выходные.

Такой путь, безусловно, возможен и в ряде случаев остается пока что единственным, но он связан с огромным объемом экспе- рихментных и вычислительных работ, требует наличия сложной, а подчас специальной аппаратуры и вызывает определенные труд­ности в анализе и синтезе получаемых результатов. Пример то­му—модель зерновой сеялки, приведенная в работе [125], со­гласно которой общее число только учтенных факторов условий работы, управления и задающего воздействия, кроме составляю­щих выходного вектора-функции, насчитывается более 15, что, естественно, делает решение данной задачи методами идентифика­ции практически невозможным. Поэтому в настоящее время при исследовании динамики сельскохозяйственных машин в большин­стве случаев используются одномерные линейные системы, не­смотря на присущие им недостатки. В связи с этим постановку задач математического моделирования, а следовательно, и задач анализа и синтеза объектов сельскохозяйственной техники во мно­гих случаях, как отмечает академик П. М. Василенко, нельзя признать корректной [105].

Большие перспективы для решения задач анализа и синтеза сельскохозяйственных машин имеют механико-статистические (комбинированные) методы, основанные на одновременном и сов­местном использовании аналитических (механико-математических) и вероятностно-статистических методов.

Механико-статистические методы значительно упрощают по­строение математических моделей (операторов) динамических сис­тем и оказываются достаточно эффективными при исследовании мобильных сельскохозяйственных агрегатов, выходными парамет­рами технологических процессов которых являются показатели до­зирования и распределения обрабатываемых материалов, а основ­ные возмущающие переменные, действующие на входе системы, представляют собой случайные процессы, обусловливающие коле­бательный характер поведения машины.

Однако следует отметить, что эти методы применительно к ис­следованиям сельскохозяйственных машин и их технологических процессов, как замечает профессор А. Б. Лурье, практически не разработаны [286]. Нам также не удалось найти работы, в кото­рых были бы освещены эти вопросы.

Основными причинами этого, вероятно, является отсутствие до недавнего времени [104] четкой классификации сельскохозяйствен­ных агрегатов как динамических систем, а также унифицирован­ных математических моделей, описывающих поведение определен­ной группы машин, выполняющих идентичные или близкие по характеру технологические процессы. Это привело, с одной сто- доны, к тому, что многие авторы [59, 75, 92, 125, 204, 242, 290] при исследовании одних и тех же или близких по назначению и выполняемому процессу машин с одинаковой постановкой задачи используют совершенно разные математические модели, причем без должного обоснования и оценки степени соответствия их реаль­ным процессам; с другой — нередко построение математических моделей, причем весьма сложных, вызывается не столько необхо­димостью применения их для решения конкретной задачи, сколько желанием автора показать свой уровень эрудиции в области ма­тематики.

Наличие унифицированных математических моделей, на наш взгляд, позволило бы, во-первых, избежать указанных выше нега­тивных явлений, во-вторых — ускорить разработку новых машин, а главное, повысить качество их еще на стадии проектирования и расчета.

Не задаваясь целью детально осветить вопросы содержания механико-статистических (комбинированных) методов исследова­ния динамических систем, покажем на примере анализа и син­теза овощной сеялки точного высева возможность и эффектив­ность их применения.